Mutation free energy calculations

Contents

A. Introduction

 Now we are entering the realm of protein design. We will take a small protein and try to make it better. Or at least more stable. In order to achieve that, we are going to carry out "alchemical" mutations during the simulations and compute the corresponding free energy changes. 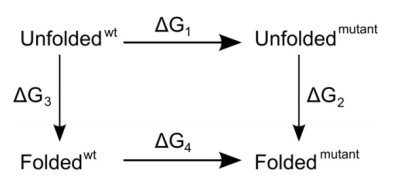If we do this both in the folded and unfolded states, and compute the difference between them, this will yield us an estimate of the difference in stability between wild type and mutant, as indicated in this thermodynamic cycle:


Experimentally, to address the same question, we would access the vertical legs of the cycle and carry out folding/unfolding experiments to determine ΔG3 and ΔG2. The difference ΔΔG = ΔG3 - ΔG2 is then the difference in folding free energy between wild type and mutant. In the simulations, this would be too demanding, as even the folding time of a small peptide can be computationally prohibitive, therefore preventing us from reliably obtaining the folding free energies ΔG3 and ΔG2 directly from the simulations for most peptides and proteins. However, we can relatively accurately obtain the mutation free energies ΔG1 and ΔG4 from "alchemical" mutations in which we morph one amino acid into another and compute the according free energy change. If we do that both in the folded and the unfolded states, we can make use of the fact that the free energy is a state variable and therefore that the sum of all four free energy values must be zero. Or, to put it differently, ΔΔG = ΔG3 - ΔG2 = ΔG1 - ΔG4. For the unfolded state, we do not really know what it looks like. So we are going to assume that it can be modeled by a small piece of unstructured peptide. In the current tutorial we will focus on the simulation preparation of a folded protein, however, an identical procedure can be applied to the short unstructed peptides as well. In fact, the free energy differences for mutations in GXG tripeptides can be precomputed for a given mutation library in a specific force field. Here you can find the precomputed ΔG values for GXG tripeptides in several force fields.


Go back to Contents

B. Preparation

We are now going to set up our first mutation simulation. The set up is a bit different from a usual gromacs set up, as we use the pmx package for this, which is an add-on to gromacs. We prepared an example based on a small protein minimal protein, to keep things simple and tractable. Of course, feel free to mutate another protein, at the risk that the simulations will likely take considerably longer. The next example assumes that you work with the prepared "peptide.pdb". If not, please rename the filenames accordingly.
First, let us have a close look at the structure and see which mutation you'd consider to be potentially stabilizing:
pymol peptide.pdb
You will see that the peptide is folded around a central tryptophan residue. It might be tempting to mutate this residue, but remember that a larger perturbation will take longer to converge in the simulation, so a smaller or more conservative change might be more promising. In addition, it is recommended not to introduce mutations that introduce charge changes. This is due to the fact that the buildup of a net charge during the morphing simulations can lead to artifacts and longer convergence times. To define where we want the mutation and to set up the morph structure we will use pmx mutate.py function. Prior to doing that, set the GMXLIB variable to point to the path containing mutation libraries. In case the paths are not yet properly set on the machine you are working on, you will need to set GMXLIB manually. Find out where the pmx source folder is and run
export GMXLIB=/home/training/Tutorials/pmx/pmx/pmx/data/mutff45
Also, it is convenient to add all the pmx scripts into your path. To do that type:
export PATH=$PATH:/home/training/Tutorials/pmx/pmx/pmx/scripts
Also, we need to activate Conda environment with the installed pmx:
conda activate pmx
Now we are ready to perform the mutations. Run the mutate.py script:
mutate.py -f peptide.pdb -o mutant.pdb -ff amber99sbmut
Choose the residue you want to mutate and what you want to mutate it into. Note that, as is frequently done in experiments, an alanine scan might be a good starting point to identify promising locations. Also, you may consider selecting a mutation for which a tripeptide value has already been precomputed. Once a mutation has been chosen, create a corresponding topology:
gmx pdb2gmx -f mutant.pdb -o conf.pdb -ff amber99sbmut -water tip3p
Here, the force-field used needs to be consistent with the force-field choice from the previous step (amber99sbmut in this case). We now have to post-process the topoloogy to add the morphing parameters:
generate_hybrid_topology.py -p topol.top -o newtop.top -ff amber99sbmut
In fact, these three steps of amino acid mutation and hybrid topology generation could also have be carried out via a web-based interface. Now we are ready to set up the simulation. First, we need to define a simulation box:
gmx editconf -f conf.pdb -o box.pdb -bt dodecahedron -d 0.9
and we fill it with water:
gmx solvate -cp box -cs spc216 -o water.pdb -p newtop
To prepare the first energy minimization download the em.mdp file and run:
gmx grompp -f em.mdp -c water.pdb -p newtop.top
If you looked carefully, you'll see that grompp warned that the system carries a net charge. In order to avoid artifacts due to a periodic charged system, we add a chloride atom:
gmx genion -s -nn 1 -o ions.pdb -nname CL -pname NA -p newtop.top
and select "13" as solvent group, so a water molecule can be replaced with a chloride ion. Now we can prepare for the energy minimization again:
gmx grompp -f em.mdp -c ions.pdb -p newtop.top -maxwarn 1
and carry out the actual energy minimization:
gmx mdrun -v -c em.pdb
Before we can set up the free energy calculation, we'll equilibrate the system by running a short simulation of the wild type peptide (eq.mdp file for equilibration):
echo 0 | gmx trjconv -s topol.tpr -f em.pdb -o em.pdb -ur compact -pbc mol
gmx grompp -f eq.mdp -c em.pdb -p newtop.top
gmx mdrun -v -nt 2 -nice 0 -c eq.gro
Note that you can also use more (virtual) cores for the simulation by providing a larger number after -nt.
Now we are ready to do the actual free energy calculation. Please have a look at the MD parameter file md.mdp. You will find a section called "Free energy control" where you will see that free energy is switched on, the initial lambda is chosen as zero, and that delta-lambda (per MD step) is set such that at the end of the simulation lamda is at 1. Therefore, we are using the "slow growth" method here. Now start the actual simulation.
gmx grompp -f md.mdp -c eq.gro -p newtop.top
gmx mdrun -v -nt 2 -nice 0 -c md.gro
Again, This will take a while. Nevertheless, the number of steps defined in "md.mdp" corresponds to only 100 ps, which is too short to expect a converged result, and therefore for an accurate free energy estimate. Therefore, to assess convergence, we suggest to carry out two validation steps: Using the approach outlined above, try to find a reasonable balance between computational effort and accuracy. Using the identified scheme, devise a scheme to systematically identify mutations that stabilize the folded structure of the peptide.

Go back to Contents

C. Free energy estimation

Slow growth thermodynamic integration (TI) approach relies on an assumption that during a transition the system remains in a quasi-equilibrium state. Therefore, integration over the dH/dl curve directly yields a difference in free energy. We have prepared a 10 ns forward and backward transitions of an S13A mutation in the TRP cage protein. Integration can be done using the gmx analyze tool. (Keep in mind that the integration for lambda ranges from 0 to 1 for the forward direction and from 1 to 0 when integrating backwards)
gmx analyze -f dhdl.xvg -integrate

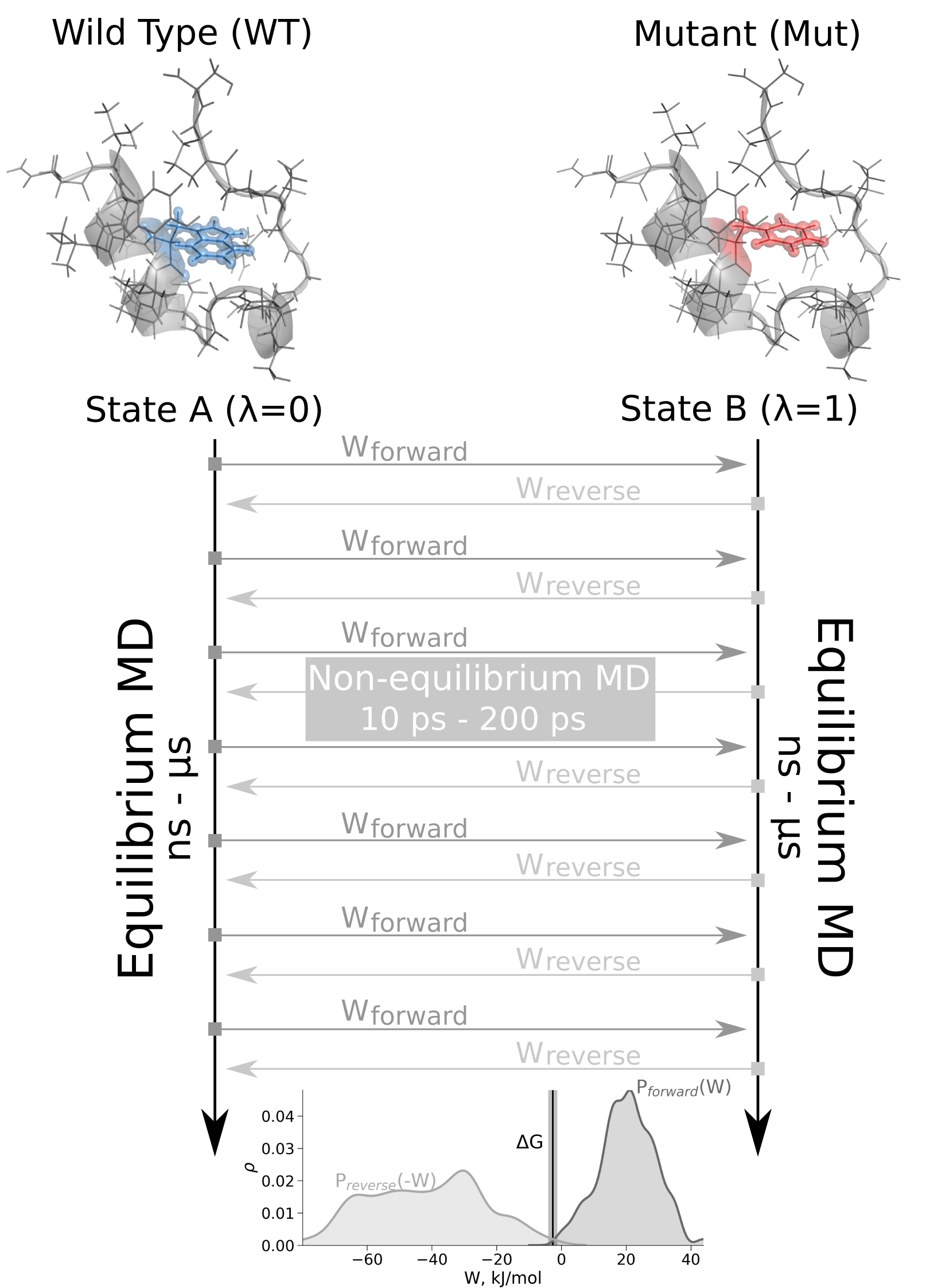
In practice, however, the slow growth TI is not frequently used. An alternative method, that does not require an assumption of quasi-equilibrium during the alchemical transition is the fast growth TI. The fast growth TI approach relies on Jarzynski's equality (when transition is performed in one direction only) or on the Crooks Fluctuation Theorem (when the transitions are performed in both directions).

The schematic representation of the non-equilibrium alchemical free energy calculations is depicted on the right. Here, free energy difference in the folded state of a protein is calculated. Firstly, two independent equilibrium simulations need to be performed by keeping the system in its physical states: WT and mutant. These simulations need to sufficiently sample the end state ensembles, as the free energy accuracy will depend on the sampling convergence. Typically the equilibrium simulations are in the nanosecond to microsecond time range. From the generated trajectories snapshots are selected to start fast (typically 10 - 200 ps) transitions driving the system in the forward (WT to mutant) and reverse (mutant to WT) directions. The work values required to perform these transitions are collected and the Crooks Fluctuation Theorem is used to calculate the free energy difference between the two states.

The archive file S13A_fast_growth.tar.gz contains two 10 ns simulation trajectories for the system in state A (eqA directory) and B (eqB directory). (In case this file appears to be too large, you can download the file with analysis folder only.) From the trajectories 100 snapshots have been extracted and a fast 50 ps simulation has been performed starting from each frame. During the simulation a system was driven from from state A to B (and vice versa) in a non equilibrium manner and the dH/dl values were recorded. pmx has utilities allowing to integrate over the multiple curves and subsequently estimate free energy differences using several approaches: Crooks Gaussian Intersection, Bennet Acceptance Ratio or Jarzynski's estimator:

analyze_dhdl.py -fA eqA/morphes/frame*/dgdl.xvg -fB eqB/morphes/frame*/dgdl.xvg -t 300 --nbins 25
The free energy estimates are summarized in the file results.dat. You can also investigate the individual work values for every transition in the forward (integ0.dat) and backward (integ1.dat) directions. How do the non-equilibrium work values compare to the quasi-equilibrium slow growth work estimates? The script also produces several plots facilitating analysis of the work distributions.

So far we have investigated only one part of the cycle involving the folded protein. To construct a double free energy difference the ΔG value for a mutation in the unfolded protein (which we approximate by a GXG tripeptide) is needed. The results for the A2S mutation in the tripeptide can be found here. The final ΔΔG value will indicate whether the mutation is stabilizing the protein in its folded state. Experimental measurements suggest that S13A mutation is mildly stabilizing (1.8 kJ/mol) Barua et al, 2008.

Go back to Contents

D. Further steps

Depending on time and interests, address one or more of the following questions:

Go back to Contents

Further references:

Go back to Contents